Mathematics
The NUbots codebase uses specific mathematical concepts and notation that are relevant to the field of robotics. In the codebase there are many uses of vectors, matrices, spaces, and transforms between spaces. A specific notation is used for these transforms for better readability. This page details how these concepts and notations are implemented in the codebase.
Linear Algebra
We currently use the Eigen C++ template library for linear algebra in the NUbots codebase. Be aware that Eigen has some common pitfalls that are listed on the Eigen pitfalls page.
Bases
A basis is a maximal set of linearly independent vectors.
In this context, bases usually span . That is, they cover three-dimensional space. Given a basis with three vectors , any three dimensional vector can be written as
where . In other words, are scalars. These scalars are unique.
If the vectors in the basis are mutually perpendicular, then they are orthogonal.
An orthonormal basis (ONB) is a basis which is orthogonal and each vector has length 1.
An example of an ONB is the standard basis
Vectors
As mentioned in the previous section, any vector can be expressed as a linear combination of the elements of a basis
The scalars are the coordinates for the vector in the basis .
In the NUbots codebase, vectors are written as rABb which denotes a vector from point to point in the basis (or space) . These are column matrices of the coordinates of the vectors
To make computations such as inner product (also called dot product) or cross product with coordinates, the vectors must be relative to the same basis.
When drawing a vector , that is a vector from to in the space , the tail is at and the head is at . Vector addition requires that the head of one vector is the same as the tail of the other. This is demonstrated here. We have that
since vector addition is commutative. This is written in code as
Eigen::Vector3d rACb = rABb + rBCb;Rotations
To describe the motion of the robot, we need a reference frame and a coordinate system.
The reference frame is the physical rigid body and the coordinate system is a mathematical concept, which is represented as a basis.
NUbots use a right-handed coordinate system to measure positions and rotations.
Rotations are defined by a 3x3 matrix. If we have a vector , that is the vector in the coordinate system , the rotation
will rotate by radians around the coordinate axis .
More on rotation matrices can be found here.
The orientation of the basis relative to can be described by three consecutive rotations about the main axis. There are 12 different orders to do these rotations in, and each triplet of rotated angles is called a set of Euler angles. In robotics, the triplet is yaw, pitch and roll (Z-Y-X).
In the NUbots codebase, we denote a rotation matrix from space to space as Rab.
The rotation matrices used for changing between spaces belong to the special orthogonal group of order 3. These all have the following properties
The first property reduces the complexity of the computation to find the inverse matrix. The second property tells us this matrix can be inverted and it preserves scale between the two spaces.
If we have a vector , that is it goes from point D to point C in a space , and we want to rotate it from space to space , we write
This is written in the NUbots codebase as rCDb = Rba * rCDa. Note that the notation is .
Homogeneous Transformations
A homogeneous transformation matrix in three dimensions is a 4x4 matrix containing a rotation component and a translation component.
If we have some rotation and a translation component , then we have a transformation matrix that transforms from space to space :
This is written in the NUbots codebase as Hba.
The vector is the vector from B (the origin of space b) to A (the origin of space a) in b space, which would be written in the codebase as rABb.
The reason for this is that if we apply the transform to some point , then will first be rotated by , giving . will then be translated by some vector according to the transformation matrix. Since is now rotated in the coordinate system, the translation vector must also be in this coordinate system. The vector is from B to A because a point (0, 0, 0) in space should be moved to the origin of in space after transformation. Thus, the translation vector is .
This is illustrated in the following diagram.
This assumes the original vector, rCAa has already been rotated into space , i.e. we have rCAb.
Finding the inverse of is made simpler by the properties of the matrix.
Transformation matrices left multiply with vectors to get a vector in the new space. This vector is rotated and then translated.
This is written in the codebase as rCBb = Hba * rCAa.
This is equivalent to
or in code,
Eigen::Vector3d rCBb = rABb + (Rba * rCAa);Vectors should only be multiplied with a transformation matrix if the last two
letters of the vector match. That is, the position they are going from should match the
origin of the space they are measured in. This means that Hab * rCBb is
valid, but Hab * rCDb is invalid. Note that the first vector is rCBb and the second is rCDb.
If you would like the vector only rotated, extract the rotational component of the transform and apply it to the vector. The spaces that the vector and rotation matrix are in should match.
Eigen::Vector3d rCDb = Hba.rotation() * rCDa;Homogeneous transformation matrices can be multiplied together to get a new homogeneous transformation matrix.
This is written in the codebase as
Eigen::Isometry3d Hca = Hcb * Hba;Unit Vectors
A unit vector is a vector with a length of 1. They are used to represent directions in space.
They are written by describing their origin, the direction they are pointing and the space they are in.
is a unit vector at B pointing towards A measured in space b.
The direction of a vector can be found by normalising it. This is done by dividing the vector by its length.
Eigen::Vector3d uABb = rABb.normalized();Unit vectors can be rotated by rotation matrices but not translated. They should not be multiplied by a homogeneous transformation matrix.
Velocity and Acceleration
The velocity and acceleration of some object is represented relative to some space.
If we have the velocity of object A moving relative to space b , then we write this in the codebase as vAb.
If we have the acceleration of object A moving relative to space b , then we write this in the codebase as aAb.
Velocities and accelerations can only be rotated, not translated. They should not be multiplied by a homogeneous transformation matrix, but they can be multiplied by a rotation matrix.
If a velocity is multiplied with time, it becomes a displacement vector.
Eigen::Vector3d rA_tAb = vAb * t;If an acceleration is multiplied with time, it becomes a velocity vector.
Eigen::Vector3d vA_tAb = aAb * t;If you only have a partial velocity or acceleration, such as velocity in the direction of an object you can represent this by labelling the target the velocity is towards.
For example would describe the velocity of B towards the point A.
Examples
Using Eigen, we define our vectors as Eigen::Vector3d, rotation matrices as Eigen::Matrix3d, and homogeneous transformation matrices as Eigen::Isometry3d. The d denotes double and instead can be f for float. Eigen::Isometry3d allows us to do computations easier than with Eigen::Matrix4d.
It allows multiplication with a Eigen::Vector3d even though the dimensions do not match. Using Eigen::Isometry3d makes it quicker to find the inverse, as it employs the techniques mentioned above. Eigen::Isometry3d has functions to individually return the rotational component of the matrix and the translation component of the matrix, by using Htw.rotation() and Htw.translation() respectively, where Htw is of type Eigen::Isometry3d. It also makes it easy to individually assign the rotational and the translational components of the matrix by using Htw.linear() = Rtw and Htw.translation() = rWTt respectively.
When we get a message that is a homogeneous matrix it will be of type mat4. This can then be cast to Eigen::Isometry3d. Let the matrix be called Htw (world to torso transform) and the message be called sensors (see: Sensors.proto). Then this is written as
Eigen::Isometry3d Htw(sensors.Htw);If you have a transformation matrix Htw (world to torso transform) and you want the matrix Hwt (torso to world transform), this is can be achieved by calling Htw.inverse(). The inverse function swaps the letter order. The returned inverse matrix is not mutable.
If you have a vector rTWf (world to torso in foot space) and you want the opposite letter order (torso to world in foot space), this is done by negating the vector, rWTf = -rTWf.
Negating does not change the space the vector is measured in.
If you have two transformation matrices and you would like to multiply them to get a new transformation matrix, the inner two letters should be identical, i.e. the same space.
Eigen::Isometry3d Htf = Htw * Hwf;This gives the foot to torso transform by multiplying the world to torso transform with the foot to world transform.
These two inner letters are cancelled, with the outer two remaining. This also works for rotation matrices.
If you have two vectors in the same space and their inner (or outer, since vector addition is commutative) letters are both the same then they can be cancelled in a similar way to the transformation matrices.
Eigen::Vector3d rXZa = rXYa + rYZa;Reference Frames
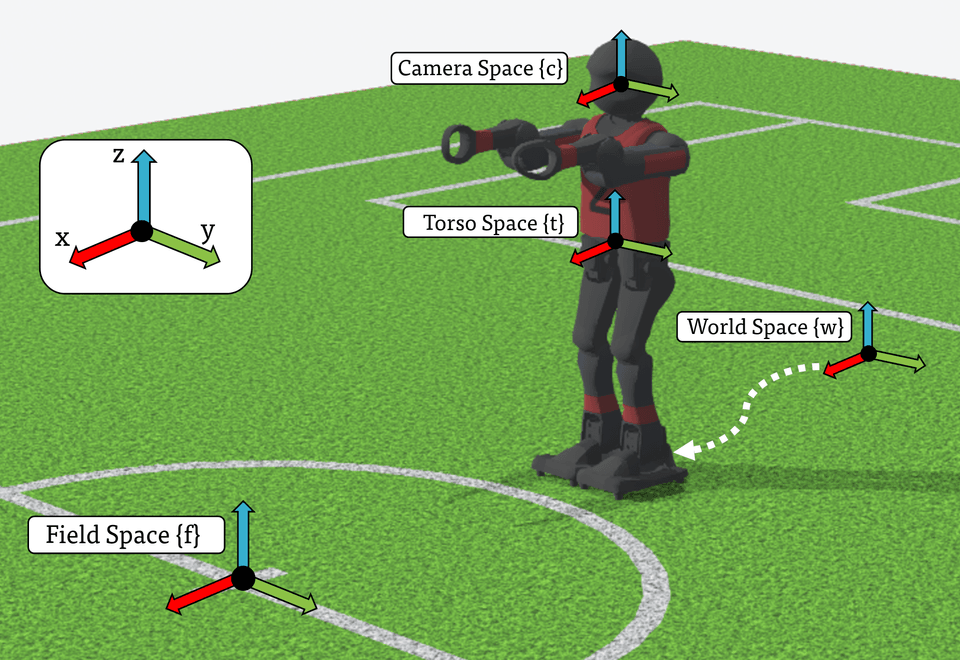
The NUbots codebase uses a number of different reference frames (spaces) for different purposes. The following is a list of the commonly used spaces in the codebase.
| Space | Letter | Description |
|---|---|---|
camera | C | Located at camera (left/right) with x pointed "outwards", y to the "left" and z "up" |
world | W | Located on the ground below the robot on startup. (Fixed inertial frame) |
torso | T | Fixed midway between the robots hip yaw joints, with x "forward", y to the "left" and z "up" |
robot | R | Located directly beneath torso projected onto the ground, with x "forward", y to the "left" and z "up" |
field | F | Located at the centre circle of the field, with x pointing towards the "own" goal and z "up" |
Summary
| Item | Description |
|---|---|
Hab | Denotes a 3D affine transformation matrix going from space to space . |
Rab | Denotes a 3D rotation matrix from space to space . |
rABb | Denotes a vector from point to point in space . |
uABb | Denotes a unit vector from point towards point in space . |
vAb | The velocity of in space . |
vABb | The velocity of towards in space . |
aAb | The acceleration of in space . |
aABb | The acceleration of towards in space . |
rXZa = rXYa + rYZa | Create a new vector from two other vectors. |
rACc = Hcb * rABb | Changing a vector from one space to another using a homogeneous transform. |
rABd = Rdc * rABc | Changing a vector from one space to another using a rotation transform |
Hba = Hab.inverse() | Inverting a matrix swaps the letter order. |
Hac = Hab * Hbc | Creating a new transform from two other transforms. |
| Euler Angles | Are of the form Z-Y-X. |
Useful Links
Spherical Coordinates
Spherical coordinates are a system of representing points in 3D space. Rather than representing points as cartesian coordinates, points are represented as , where r is radial distance, is the polar angle, and is the azimuthal angle.
Spherical coordinates can be calculated from cartesian coordinates using the follow equations:
Cartesian coordinates can be calculated from spherical coordinates using the follow equations:
A vector representing a point in the spherical coordinates would be written as , which would be sABb in the codebase.
In order to ensure a unique representation of coordinates, the following restrictions are enforced on spherical coordinates:
Reciprocal Distance
A common variation on spherical coordinates in our codebase is to use reciprocal distance. If a vector has spherical coordinates , then a vector in spherical coordinates with reciprocal distance has coordinates .
This is used in the vision detectors and localisation when representing the distance from the camera to an object. Using reciprocal distance also means our covariance (our uncertainty in our measurement) scales better with distance. The further away an object is the less certain we are about out measurement of it.
If is the vector in spherical coordinates, then is the same vector in spherical coordinates, but with reciprocal radial distance.
Interpolation
Given a set of data points, often we want to find a function that contains all these points, which we call an interpolant. Interpolants are commonly polynomials, because they can approximate complex curves with a few points, with relatively low computational costs. Interpolant polynomials can be affected by Runge's phenomenon, where the interpolant is locally accurate for the given data points but has oscillations issues beyond these points. A further issue with interpolants is uniqueness - if there are too few constraints then there may be an infinite number of interpolants, and if there are too many constraints then there may not be a solution. Generally, for distinct points, there is a unique polynomial of degree that interpolates the points. Polynomials of degree higher than may have aliasing issues where the interpolant is unnecessarily 'wiggly' between points.
Splines
Rather than have one global polynomial, it can be useful to use piecewise polynomials, connected at their edges. These so-called splines are all defined locally around the interpolation points, and can avoid Runge's phenomenon. Splines are used in the Quintic Walk Engine.
Every pair of consecutive points on the graph has an associated polynomial that is plotted in the range between those two points.
The Quintic Walk specifically uses quintic splines. This means that each polynomial is of the form
For , where is the number of interpolation points.
These particular quintic splines have interpolation points . They must satify the conditions
- is a polynomial in for each
- and for each
- for each
- for each
- and
- and
These conditions result in smooth joints between each polynomial, meaning the position, velocity and acceleration at those joints is the same for both polynomials. Each data point has an x and y value, as well as first and second derivative value. The conditions above ensure the splines satisfy the given values for each data point.
Units
See the glossary.

